
 Версия сайта для слабовидящих
Версия сайта для слабовидящих
 |
 |
 |
 |
 |
 |
 |
| школа | учеба | люди | партнеры | досуг | фотобанк | форум |
| олимпиады |
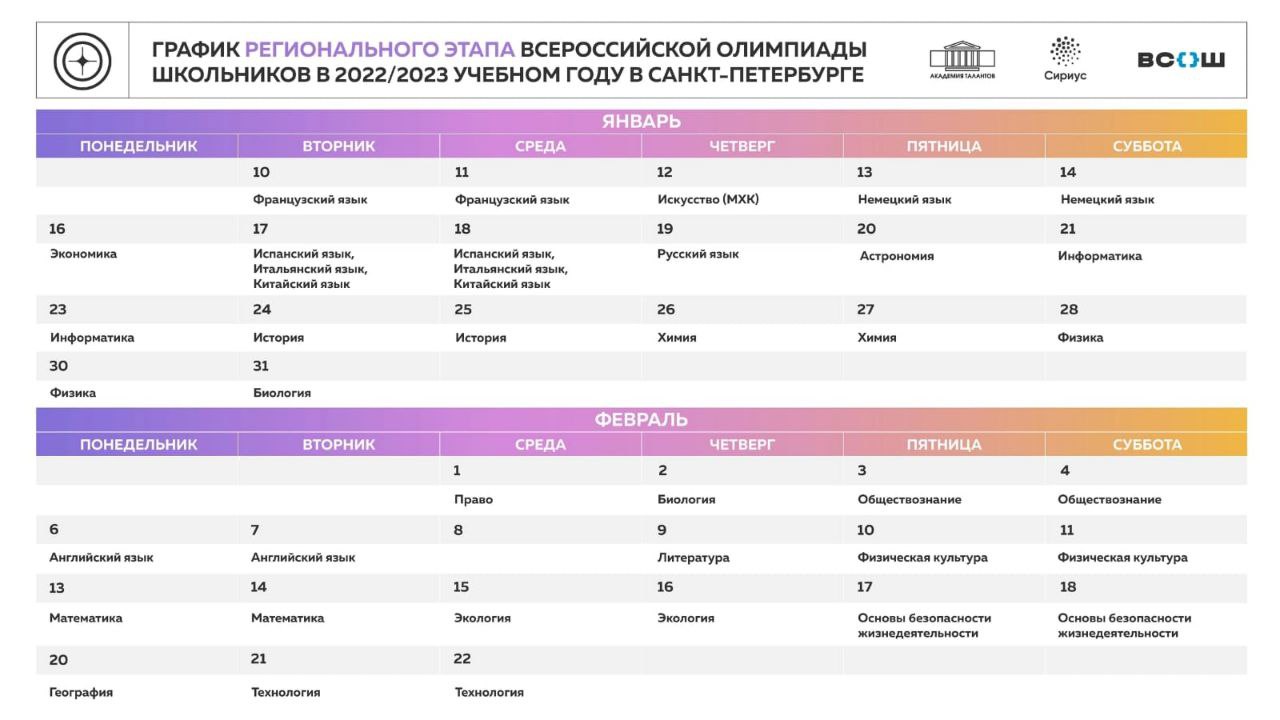
Гимназисты каждый год участвуют в олимпиадах по всем возможным предметам: по математике, физике, химии, информатике, географии, истории, биологии, английскому, немецкому и русскому языкам. Почти всегда они занимают призовые места как минимум в районном туре. Ниже приводятся списки победителей олимпиад во всех турах и по всем предметам.
Ежегодные олимпиады школьников по латинскому языку проводятся под эгидой различных учебных заведений Москвы (за исключением олимпиады 2002 г., которая проходила в Петербурге, в нашей гимназии). Ученики Санкт-Петербургской классической гимназии участвуют в олимпиадах с 1999 г. и регулярно оказываются в числе призеров.
Certamen della Tuscia — ежегодное национальное итальянское состязание школьников, которое с 1996 г. проводится в г. Витербо под эгидой местного университета и классического лицея им. Марио Буратти.
Pythian Contest — ежегодное международное состязание для школьников по греческому языку и культуре, проводившееся Европейским культурным центром г. Дельфов (European Cultural Centre of Delphi) через систему национальных конкурсов.
Европейская олимпиада по древнегреческому языку — ежегодное международное состязание для школьников выпускных классов; проводится с 2000 г. в 16 европейских странах под эгидой Министерства образования Греции, Центра по распространению греческого языка (ΟΔΕΓ) и ассоциации Euroclassica.
Традиционная Олимпиада по лингвистике и математике впервые состоялась в 1965 году и до 1982 года регулярно проводилась на базе отделения структурной и прикладной лингвистики филологического факультета Московского государственного университета им. М.В. Ломоносова. В 1988 году она была возобновлена в МГИАИ. С 1989 года традиционную Олимпиаду проводят совместно МГУ и РГГУ. В последнее время география Олимпиады расширяется: уже несколько лет она проходит в Санкт-Петербурге, в Болгарии, в Нидерландах.
IOL — одна из двенадцати Международных Научных Олимпиад. Каждый год на этой олимпиаде собираются молодые лингвисты из разных стран, чтобы попробовать себя в разрешении наиболее сложных проблем языкознания.
Математическая олимпиада «MATHMAN» проводится ежегодно для седьмых классов «Международным (русско-турецким) лицеем» №664. В «MATHMAN» принимают участие команды, что позволяет выявить средний уровень подготовки в той или иной школе; в то же время каждый участник точно видит свой собственный уровень. Тест включает в себя 50 вопросов по алгебре и геометрии школьного курса; у каждого вопроса есть 5 возможных вариантов ответа, из которых только один является верным. За каждый правильный ответ начисляется 1 очко, за каждый неправильный — отнимается 0,25 баллов. Награждаются не только юные участники, занявшие призовые места, но и их учителя.
«Кенгуру» — международная математическая олимпиада для школьников, которая проводится в России с 1997 года. «Русский Медвежонок» — аналогичная олимпиада по русскому языку, существующая с 2000 года.
Турнир им. М. В. Ломоносова — ежегодное многопредметное соревнование по математике, физике, наукам о Земле, химии, биологии, истории, лингвистике, литературе. Задания ориентированы на учащихся 7-11 классов. Программа во всех местах одинакова. Конкурсы по всем предметам проводятся одновременно в разных аудиториях в течение 5 часов. Дети имеют возможность свободно переходить из аудитории в аудиторию, самостоятельно выбирая предметы и время.